even and odd functions integrals | DEFINITE INTEGRALS OF ODD AND EVEN

Entourage: With Seo Kang-joon, Cho Jin-woong, Lee Kwang-soo, Sohee. South-Korean version of 'Entourage' (2004). This is the story of a handsomely famous celebrity who depends on his three friends and agency's boss who try to help him in his struggles as an actor and a man.

even and odd functions integrals*******Sometimes we can simplify a definite integral if we recognize that the function we’re integrating is an even function or an odd function. If the function is neither even nor odd, then we proceed with integration like normal.Definite integrals of even and odd functions. Learn math Krista King April 17, 2018 .Apply the integrals of odd and even functions. We saw in Module 1: Functions and Graphs that an even function is a function in which [Math Processing Error] f ( − x) = f ( x) for all [Math Processing Error] x in the domain—that is, the graph .Now, let’s dig into integrals of even and odd functions! Let f be an integrable function on some closed interval that is symmetric about zero — for example [ − a, a], for a ≥ 0. If f is even, then: .

Fill in the following table: the product of an (even/odd) function with an (even/odd) function is an (even/odd) function. You may assume that both functions are defined for all real . TheMathCoach talks about odd and even functions. The video covers: The definitions for even and odd functions, Integration of odd and even functions over .Learning Objectives Apply the basic integration formulas. Explain the significance of the net change theorem. Use the net change theorem to solve applied problems. Apply the integrals of odd and even functions.Definte Integrals of Odd and Even Functions. If f (x) is an odd function, If f (x) is an even function, Evaluate each of the following integrals. Example 1 : Solution : Let f (x) = x3 + 3x. f (-x) = (-x)3 + 3 (-x) f (-x) = -x3 - 3x.

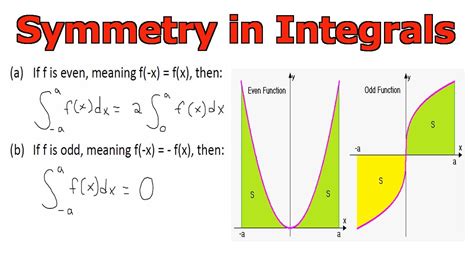
integrals of even and odd functions. Proof. Since the definite integral is additive with respect to the interval of integration, one has. Making in the first addend the substitution t= −x, dt=−dx t = . EVEN AND ODD FUNCTIONS A function is said to be even if it will remain unchanged after replacing x by –x. Otherwise, it is an odd function.Theorems on the i.even and odd functions integrals DEFINITE INTEGRALS OF ODD AND EVEN Symmetry appears throughout mathematics in many different forms, and its use often leads to insights and efficiencies. Here we use the symmetry of a function to simplify integral calculations. Section 1.1 introduced the symmetry of even .If a function is even then it is symmetrical with respect to the y-axis. Therefore when you integrate it you only need to integrate half of it (greater than zero part or less than zero part) and double your answer. If the function is odd, it is also symmetric with respect to the y-axis expect this time one side is the negative of the other.

even and odd functions integrals For even functions the integral from -a to a is . In this video I go over the theorem on integrating symmetric functions which greatly simplifies integration.Integrating Even and Odd Functions - Key takeaways. We can classify some functions into even functions or odd functions. Even functions are functions such that for every x in its domain. Odd functions are functions such that for every x in its domain. If is an even function that is integrable on the interval then . In this section we look at how to integrate a variety of products of trigonometric functions. These integrals are called trigonometric integrals.They are an important part of the integration technique called trigonometric substitution, which is featured in Trigonometric Substitution.This technique allows us to convert algebraic expressions that we may not be .The theorem of “Integration of Even and Odd Functions” is a way to find integrals for odd and even functions. It’s a method that makes some challenging definite integrals easier to find. In order to use it, you have to be evaluating a function over an interval that’s either symmetric about the origin or symmetric about the y-axis [1].

Integrating Even and Odd Functions. We saw in Functions and Graphs that an even function is a function in which \(f(−x)=f(x)\) for all \(x\) in the domain—that is, the graph of the curve is unchanged when \(x\) is replaced with \(−x\). The graphs of even functions are symmetric about the \(y\)-axis.We will need the following fact about the integral of an odd function over a ’balanced’ interval [−L, L]. L If f (t) is odd then f (t) dt = 0. −L This fact becomes clear if we think of the integral as an area (see Fig. 2). Multiplying Even and Odd Functions When multiplying even and odd functions it is helpful to think in terms of

In this video, we are finding the value of a definite integral of an odd function x^4 sin(x), with limits opposite of each other. Since the function is odd, .The "what is" part has already be answered by Alex White. The "how does it help in integration" part is easy: If your integration interval is symmetric around $0$ (which especially includes integration over all of $\mathbb R$), then the integral over any integrable odd function is zero, no exception. Therefore as soon as you've found that your integrand is odd and your .5.4.1 Integrating Even and Odd Functions Symmetry appears throughout mathematics in many different forms, and its use often leads to insights and efficiencies. Here we use the symmetry of a function to simplify integral calculations. Is it because we're limited by the need to prove that the integral of that (odd) function is even? integration; functions; Share. Cite. Follow asked Apr 12, 2015 at 6:00. AstroInt AstroInt. 333 1 1 gold badge 2 2 silver badges 11 11 bronze badges $\endgroup$ 1Tour Start here for a quick overview of the site Help Center Detailed answers to any questions you might have Meta Discuss the workings and policies of this siteWe saw in Module 1: Functions and Graphs that an even function is a function in which [latex]f(\text{−}x)=f(x)[/latex] for all [latex]x[/latex] in the domain—that is, the graph of the curve is unchanged when [latex]x[/latex] is replaced with −[latex]x[/latex]. The graphs of even functions are symmetric about the [latex]y[/latex]-axis. An odd function is one in which [latex]f(\text{−}x . Even Odd Functions - Integration C5 S5 v3 \(\ds \int_{\map \phi a}^{\map \phi 0} \map f x \rd x\) \(=\) \(\ds \int_a^0 \map f {-u} \paren {-1} \rd u\) \(\ds \) \(=\) \(\ds \int_0^a \map f {-u} \rd u\) Integral of x^2/(1+2^sin(x)) from -1 to 1, Integral property involving even and odd functions. Subscribe to @blackpenredpen for more fun calculus videos!

Definte Integrals of Odd and Even Functions. If f(x) is an odd function, If f(x) is an even function, Evaluate each of the following integrals. Example 1 : Solution : Let f(x) = x 3 + 3x. f(-x) = (-x) 3 + 3(-x) f(-x) = -x 3 - 3x. f(-x) = -(x 3 + 3x) f(-x) = -f(x) .

Contact the Registrar’s Office of your chosen OLFU Campus and inform them of your desire to re-enroll at OLFU. You may reach the Registrar via the following options: A. The OLFU Concierge (virtual via Zoom)

even and odd functions integrals|DEFINITE INTEGRALS OF ODD AND EVEN